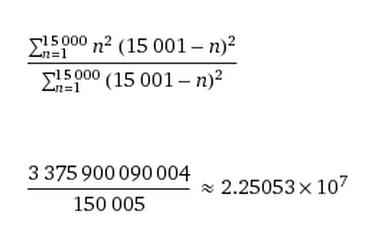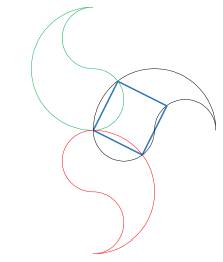|
#1 - 08-08-2011 16:48:49
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Il faut être carrré !
Soit un carré de 15 m de côté, quadrillé par des lignes parallèles à ses côtés, tracées tous les millimètres. Quelle est l'aire moyenne de tous les carrés qui ont leurs sommets situés aux nœuds du quadrillage ?
Donner une réponse approchée, arrondie au m².
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 08-08-2011 19:01:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Il fatu être carré !
22,51 m^2 Avec excell mais il n'aime pas les grand nombres
Avec wolfram ça marche mieux :
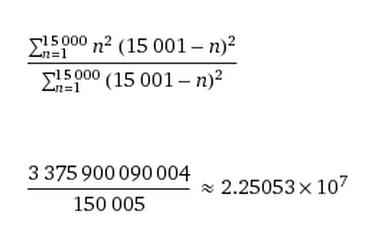
soit 22,5053 m^2
#3 - 08-08-2011 20:34:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Il faut être arré !
Vu la finesse du pas, ça doit pas faire une grosse différence si on prend une intégrale plutôt que le discret.
Sauf erreur, le résultat donne C²/10, soit 22.5m² pour un carré de 15 m de coté.
#4 - 08-08-2011 23:49:11
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
#5 - 08-08-2011 23:54:33
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
il faut être caeré !
En mm², c'est une quasi bonne réponse... Les deux premiers chiffres sont suffisants pour la réponse en m². Bravo looozer !
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#6 - 09-08-2011 00:44:55
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Il faut être craré !
Après une feuille excel bien rempli je tombe sur 22,499 m² en moyenne.
#7 - 09-08-2011 08:44:37
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Il fautt être carré !
Bonjour,
Le quadrillage fait 15000 x 15000: on va poser n=15000.
Je vais appeler S, la somme pour k variant de 1 à n (je ne sais pas écrire les beaux sigmas habituels).
On a:
- 1² carré de n par n,
- 2² carrés de n-1 par n-1,
- 3² carrés de n-2 par n-2,
- ...
- k² carrés de n+1-k par n+1-k,
- (n+1-k)² carrés de k par k,
- ...
- n² carrés de 1 par 1.
On a donc une aire moyenne de:
A = S[k²(n+1-k)²] / S[k²]
Or (n+1-k)² = (n+1)² - 2(n+1)k + k²
Donc A = (n+1)² - 2(n+1) Skkk/Skk + Skkkk/Skk
De plus, on a (merci Google, tu es mon ami !!):
- Skk =n(n+1)(2n+1)/6,
- Skkk =n²(n+1)²/4,
- Skkkk =n(n+1)(2n+1)(3n²+3n-1)/30.
Donc A = (n³+4n²+6n+4) / (2n+1) / 5.
AN: n=15000
Je n'ai pas la possibilité de calculer A, mais on voit que, lorsque n tend vers l'infini, alors A peut s'approximer à n²/10.
Comme 15000, c'est "presque l'infini", on devrait avoir A = 22,5 m².
Bonne journée.
Frank
Edit 1: Je me suis planté 1 / 2 / 5 fait 1 / 10 et pas 0,4. Du coup, je trouve aussi 22,5 m².
Edit 2: Je n'ai pas pris en compte les carrés dont les côtés ne sont pas parallèles au quadrillage initial; donc j'ai faux.
#8 - 09-08-2011 10:43:27
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
il fait être carré !
En considérant les positions possibles du coin supérieur gauche d'un carré de n millimètres de coté, on voit qu'elles sont dans un carré de 15000-n de coté.
la formle de l'aire moyenne en m² est donc :
∑15000n=0(15000−n)2(n1000)2∑15000n=0n2
le calcul avec WolframAlpha donne 22 m²
#9 - 09-08-2011 11:56:17
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Il afut être carré !
Il doit y avoir une ambiguïté dans l'énoncé, seul looozer a trouvé la même aire que moi. Tous les autres trouvent 22 environ. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#10 - 09-08-2011 12:02:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Il fauut être carré !
Dans mon raisonnement, il y a un carré de 15000 mm de côté, 4 carrés de 14999mm de côté
15000 : 1
14999 : 2^2=4
14998 : 3^2=9
14997 : 4^2=16
....
1 mm de côté : 15000^2 carrés possibles
la somme des surfaces est est donc la somme des produits (15001-n)^2 x n^2
le nombre de carrés est la somme des carrés de 1 à 15000
La moyenne est le quotient.
#11 - 09-08-2011 12:16:49
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
il fzut être carré !
Intéressant 
Edit: Suite à un MP de Saint-Pierre, je m'aperçois que je n'ai compté que les carrés dont les côtés sont parallèles aux bords du grand côté ce qui donne environ 22,51 soit 23 arrondi au m^2 le plus proche.
Reprenons donc le raisonnement.
On a donc dessiné un grand carré de 15000x15000 petits carrés élémentaires.
Je fais le raisonnement avec NxN pour plus de généralité.
Je considère les "carrés de base" dont les côtés sont parallèles aux côtés du carré de base.
Il n'y a qu'1 carré de base NxN dessiné.
Il y a 4 carrés de base (N-1)x(N-1) dessinés (on a 2x2 choix pour le somment en haut à gauche)
Il y a 9 carrés de base (N-2)x(N-2) dessinés (on a 3x3 choix pour le somment en haut à gauche)
...
Il y a NxN carrés de base 1x1 dessinés.
Considérons maintenant les carrés inclinés.
Dans le carré de NxN je fais se déplacer le coin supérieur gauche le long de l'arête supérieure. Le premier carré, de NxN correspond au coin en haut à gauche. Le sommet se déplace sur l'intersection suivante, les 3 autres coins glissent sur leur arête pour conserver le carré carré. On obtient un carré de côté √(N−1)2+12) et de surface (N−1)2+12. On continuant de faire glisser les sommets sur les arêtes du carré NxN on obtient des carrés de surface (N−2)2+22,(N−3)2+32,.... Pour ce carré de base NxN on obtient donc N carrés dont la somme des surfaces fait ∑N−1k=0k2+(N−k)2
Donc, soit Ni le nombre de carrés tracés pour une taille de carré de base i x i. Ni=(N+1−i)2.i.
Ces Ni carrés contribuent à la surface globale S de Si=(N+1−i)2.∑i−1k=0k2+(i−k)2
Si=13.(N+1−i)2(2i3+i)
Posons:
P1(N)=N(N+1)2P2(N)=N(N+1)(2N+1)6P3(N)=S1(N)2=(N(N+1))24P4(N)=N(N+1)(2N+1)(3N2+3N−1)30P5(N)=N2(N+1)2(2N2+2N−1)12
La somme vaut donc: S(N)=∑N1Si=13∑N1[(N+1)2−2(N+1)i+i2][2i3+i]
S(N)=13(2P5(N)−4(N+1)P4(N)+(2N2+4N+3)P3(N)−2(N+1)P2(N)+(N+1)2P1(N))
Le nombre total de carré vaut: C(N)=∑N1Ni=(N+1)2P1(N)−2(N+1)P2(N)+P3(N)
Pour 15000, cela donne: S(15000)=126 613 134 844 875 066 251 500, C(15000)=4 219 875 093 752 500 et M=30004000,6 mm^2 soit 30m^2 arrondi au plus proche.
Merci pour cette énigme.
Je suis enfin venu à bout des calculs. Un peu de calcul ne peut pas faire de mal 
#12 - 09-08-2011 14:03:34
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
Il faut être caré !
dans une grille de taille n, il y a (n−i+1)2 carrés de taille i, (que l'on peut voire en regardant un coin qui se deplace dans la grille restante).
ici n = 15ooo, on a donc :
15000∑i=1i2∗(15001−i)2/15000∑i=1(15001−i)2
wolfram me donne 22.5
#13 - 09-08-2011 14:46:08
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Il faut être carré
Bon, cet exercice va faire débat... looozer, comment as-tu fait pour trouver comme moi ? 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#14 - 09-08-2011 15:45:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Il aut être carré !
Le 22,5 que j'ai donné est une limite inférieure.
#15 - 09-08-2011 17:12:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Il fatu être carré !
je suis curieux de savoir quelle autre valeur on peut trouver... Tout le monde connait la notre après tout.
#16 - 09-08-2011 17:45:32
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Il faut être arré !
Voici ma méthode:
Je compte tous les carrés dont les côtés sont parallèles à ceux du carré de départ.
1 carré d'aire 15000²
4 carrés d'aire 14999²
9 carrés d'aire 14998²
...
14998² carrés d'aire 9
14999² carrés d'aire 4
15000² carrés d'aire 1
J'en compte 1125112502500 avec une aire moyenne de 22505250 mm²
Dans chacun des carrés précités, je construis tous les carrés dont les côtés sont obliques et dont les sommets appartiennent à son périmètre.
Pour un carré de côté n, on en compte n-1
Exemple avec n=5 :
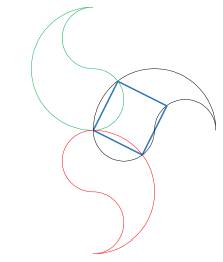
Je calcule l'aire de chacun en utilisant Pythagore.
J'en compte 4,21875 x 10^15 (soit 3750 fois plus que les autres) pour une aire moyenne de 30006000 mm²
La moyenne générale est, sans surprise, très près de la seconde moyenne : 30004001 mm²
#17 - 09-08-2011 18:46:07
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
il fauy être carré !
J'ai corrigé mon post initial directement pour prendre en compte les carrés inclinés. Pas de la tarte tout ça...
#18 - 09-08-2011 19:21:28
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
il faut êtte carré !
Je crois que je trouve comme les autres avec :
84397502250137501250000=22,5053...
#19 - 09-08-2011 19:50:14
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Il faut êtree carré !
Vous oubliez quelque chose... rivas et looozer l'ont bien vu, eux.
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#20 - 10-08-2011 11:47:21
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
il faut êrre carré !
Soit (a,b) le vecteur qui permet de définir le réseau de carré à l'intérieur du carré de 15m.
a et b sont des entiers positifs tel que a + b < 15001 (pour éviter les carrés trop grand) et a > 0 (pour éviter de compter certains carrés deux fois).
Le réseau le plus fin est défini par le vecteur (1,0) et plus gros par (15001, 0).
a varie de 1 à 15000 et b varie de 0 à (15000 - a).
L'air des carrés vaut a²+b² (puisque le coté vaut rac(a²+b²) ).
Il n'y a plus qu'à compté les carrés pour chaque réseau défini par (a,b), qui sont au nombre de (15000-a-b)².
La somme des aires pondérée par le nombre de carré par réseau divisé par la somme des nombres de carrés par réseau donnera la moyenne.
Aire moyenne=∑15000a=1 ∑15000−ab=0 (a2+b2) (15001−a−b)2∑15000a=1 ∑15000−ab=0 (15001−a−b)2
Maintenant, il faut faire le calcul...
Si je dois donner une valeur arrondie au m², je dirais 0 puisque les carrés d' 1mm² sont beaucoup plus nombreux que ceux de plus d'1m².
#21 - 11-08-2011 15:24:49
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Il faut être ccarré !
En effet j'ai omis les carrés en biais 
Je recommence le calcul (on exclut les carrés réduits à un point). On utilise le Théorème de Pythagore on notant p et q les cotés du triangle rectangle (l’hypoténuse étant le coté du carré)
∑15000n=1∑p+q=np<n(15001−n)2(p2+q2)1000000∑15000n=1∑p+q=np<n(15001−n)2=∑15000n=1∑n−1p=0(15001−n)2(p2+(n−p)2)1000000∑15000n=1n(15001−n)2=1500200035000000≃30m2
Le calcul pourrait se simplifier mais WolframAlpha fait très bien le travail tout seul 
#22 - 11-08-2011 17:12:54
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
il fait être carré !
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#23 - 11-08-2011 17:17:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Il fuat être carré !
Effectivement, je n'ai pas pensé un instant aux carrés en biais...
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum