Je me demandais effectivement ou étaient passés les matheux de P2T .
J'ai bien essayé de les motiver avec mon problème de  Sudoku en couleur, mais sans beaucoup de succès auprès de ceux-ci. Le problème reste encore ouvert.

Merci de contribuer à la relance .

En ce qui concerne ton énigme, je pense avoir les valeurs des rayons de tes billes :
                               r1 = (V3) / 2        et         R2 = V3

Le coté de ta boîte pourrait valoir :
                         c = 3 (V3 + V2) / 2,    soit    ~ 4.7819396555,
mais sous toute réserve .

Quant au volume de ton parallélépipède, ça se complique... on verra peut-être une prochaine fois.

C'était juste pour faire avancer le schmilbilibili, et que tu ne te sentes pas trop seul !

EDIT : décidément, je ne suis pas très doué pour ce genre de calcul...

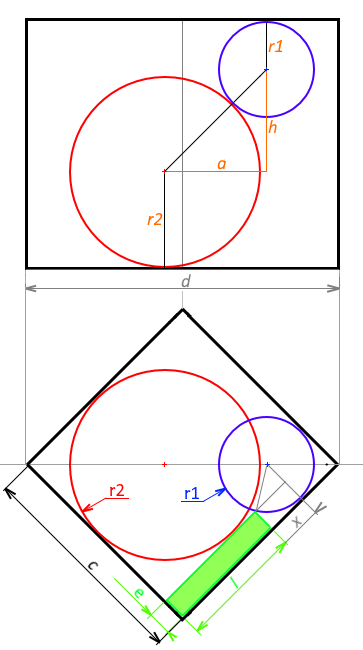
Rayons des boules: v1 = pi.V3 / 2 => r1 = V3 / 2 et: v2 = 4.pi.V3 => r2 = V3
Arête du cube: a.V3 = (r1 + r2).(1 + V3) => a = 3.(1 + V3) / 2 = 4,09808 env.

Le plus grand parallélépipède rectangle est un des quatre suivants:

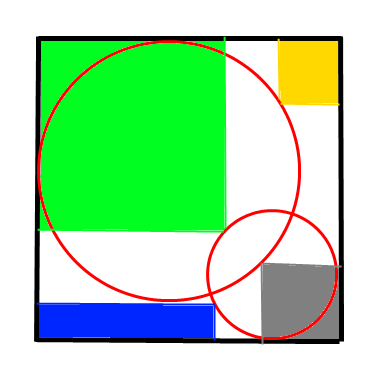
Calculons chacun des ces quatre volumes:

Vert: H = a - 2.r2 = (3 - V3) / 2 = 0,63397 env.
et: l = L = 1 + V3 = 2,73205 env.
d’où: V(vert) = 3 + V3 = 4,73205 env.

Gris: H = a - 2.r1 = (3 + V3) / 2 = 2,36603 env.
et: l = L = (V6 + V2) / 4 = 0,96593 env.
d’où: V(gris) = (9 + 5.V3) / 8 = 2,20753 env.

Orange: H = a = 3.(1 + V3) / 2 = 4,09808 env.
et: l = L = V3 / 2 = 0,86603 env.
d’où: V(orange) = 9.(1 + V3) / 8 = 3,07356 env.

Bleu: H = a = 3.(1 + V3) / 2 = 4,09808 env.
l = a - 2.r2 = (3 - V3) / 2 = 0,63397 env.
et: L = V3 + 3/2 - V(3V3 - 9/2) = 2,39769 env.
d’où: V(bleu) = 9.(1 + V3 / 2 - V(V3-3/2)) / 2 = 6,22939 env.
(qui est le volume maximal de ces quatre prismes)

Mais il y a peut-être d'autres grands prismes qui m'ont échappé.

NB: Je n’ai pas compris la mention ‘’V5 – 1 est l'écriture d'un nombre exacte’’.

Edit: Mise à jour générale des valeurs (fausses au départ).

Dont acte .
Je me suis refait un petit dessin :
                 
En exprimant c dans le sens horizontal : c = r1 + r2 + (a * V2) / 2,
                       et dans le sens vertical : c = r1 + r2 + h
je tombe sur
                                    c = 3 * (1 + V3) / 2 = 4.0980762

Si je ne me trompe, le plus grand parallélépipède, il pourrait avoir
une longueur   L = c,                         L = 4.0980762
une épaisseur  e = c - 2 * r2             e = 0.6339746
et une largeur  l = c - r1 - x .
Je n'ai pas obtenu d'expression simple pour x...
Je tente :                                          x = 0.8343575

Ce qui donnerait :                              v = 6.2293899

Je n'ai jamais été très doué pour les manipulations de formules ni pour les calculs numériques .
Je m'attend donc à être renvoyé une nouvelle fois dans les cordes !

Pas de problème, j'aurais au moins contribué à la vie de ton énigme, qui m'a occupé un bon bout de temps .

Voilà voilà



Volume = 30,3221360734996


5,01909782242685 X 1,55499620728909 X 3,88512322621129

@+

Je m'étais pris les pieds dans les racine

J'espère que c'est enfin ça :

V = 11,6423829859068 = 4,4351935184407 X 0,971091903302946 X 2,70314271087182

@+

Salut UneCoudée

Je trouve un volume max d’environ 6,22939, dans l’unité de tes billes.
Ou [18+9√3+9(1-√3)√(√3)]/4, qui est vilain.

6 emplacements dans la boite, 3 simultanés possibles. Pas mieux.

Bonjour ,

Afin de venir à bout du problème , je joins le dessin de Jackv .

Encore un petit effort !

http://www.prise2tete.fr/upload/Jackv-BoiteABilles.png

bonjour ;

@Franky1103 :  et de trois ! bravo !  par contre tu as fait une erreur de signe devant le grand radical . ( en recopiant sans doute , et dans les 2 postes )

@Bastidol : non ; ni pour l'approximation qui correspond au résultat numérique , ni pour la formule $9.\sqrt3 + 8$ qui , elle , donne une valeur : 23.588...inexacte elle aussi

bonjour;

@Batisdol :

tu es à environ   7 ou 8 centièmes , mais ce n'est toujours pas la bonne formule .

@unecoudée
Effectivement, c'est une erreur de recopie que j'ai corrigée.
Merci pour cette énigme "casse-tête".