Enigme Dix moyennes consécutives @ Prise2Tete

Vasimolo · #1

Nouveau venu sur ce forum , je propose une petite énigme

Dix collégiens sont assis autour d'une table et chacun choisit un nombre qu'il révèle à ses voisins de gauche et de droite de façon à ce que chaque élève récupère deux nombres . Les élèves annoncent alors à tour de rôle ( en tournant dans le sens des aiguilles d'une montre ) la moyenne des deux nombres qu'on leur a confiés et bizarrement on entend : 1 ; 2 ; 3 ;... ; 8 ; 9 ; 10 . Peut-on retrouver les nombres choisis par les élèves ?

J'espère qu'elle vous plaira !

Vasimolo

Bamby2 · #2

sympa en effet
la serie donne donc :
6
-3
-2
9
10
1
2
13
14
5

dhrm77 · #3

oui...
les nombres choisis sont :
5, 6, -3, -2, 9, 10, 1, 2, 13, et 14.

gabrielduflot · #4

Soit a,b,c,d,e,f,g,h,i et j les nombres qu'ont choisi les 1O élèves. Alors on a
les 10 équations suivantes
(a+c)/2=1; (b+d)/2=2; (c+e)/2=3; (d+f)/2=4; (e+g)/2=5; (f+h)/2=6; (g+i)/2=7; (h+j)/2=8; (i+a)/2=9 et (b+d)/2=10

d'où
1)a+c=2
2)b+d=4
3)c+e=6
4)d+f=8
5)e+g=10
6)f+h=12
7)g+i=14
8)h+j=16
9)i+a=18
10)j+b=20

Si on fait fait le calcul sur la ligne 9 - la ligne 7 + la ligne 5 - la ligne 3 + la ligne 1 nous donne 2a=18-14+10-6+2=10 d'où a=5; c=-3; e=9; g=1; i=13 et
Si on fait fait le calcul sur la ligne 10 - la ligne 8 + la ligne 6 - la ligne 4 + la ligne 2 nous donne 2b=20-16+12-8+4=12 donc b=6; d=-2; f=10; h=2; j=14

Autleaf · #5

Celle-ci est à ma portée !

Ce problème revient à résoudre un système linéaire 10*10.
En posant a,b,c,...,j les nombres donnés par les élèves, le système est :
[TeX]\begin{pmatrix}
1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\
1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\
\end{pmatrix}*\begin{pmatrix}
a\\
b\\
c\\
d\\
e\\
f\\
g\\
h\\
i\\
j\\
\end{pmatrix}=\begin{pmatrix}
1\\
2\\
3\\
4\\
5\\
6\\
7\\
8\\
9\\
10\\
\end{pmatrix}[/TeX]
Pour obtenir la solution, il faut calculer l'inverse de M (inversible car det(M)=3), et le résultat est
[TeX]\begin{pmatrix}
a\\
b\\
c\\
d\\
e\\
f\\
g\\
h\\
i\\
j\\
\end{pmatrix}=M^{-1}*\begin{pmatrix}
1\\
2\\
3\\
4\\
5\\
6\\
7\\
8\\
9\\
10\\
\end{pmatrix}[/TeX]
Ce qui donne [latex]\begin{pmatrix}
10/3\\
1/3\\
-8/3\\
13/3\\
4/3\\
-5/3\\
16/3\\
7/3\\
-2/3\\
19/3\\
\end{pmatrix}[/latex]

Je pense qu'ils se sont concertés

PS : Pas évident la syntaxe LateX quand on a jamais fait...

Palin01 · #6

La réponse se trouve en faisant 2 systèmes de 5 équations à 5 inconnus et on trouve ça (avec en orange le nombre choisi par l'élève et en blanc le nombre annoncé à la classe) :

Merci pour cette énigme sympathique .

scrablor · #7

6 -3 -2 9 10 1 2 13 14 5

SangFu · #8

Les réponses:
Élève 1: 3
Élève 2: -3/2
Élève 3: -1
Élève 4: 9/2
Élève 5: 5
Élève 6: 1/2
Élève 7: 1
Élève 8: 13/2
Élève 9:7
Élève 10:5/2

Ainsi:
l'élève 1 dira 1 car (5/2)-(3/2)=1
l'élève 2 dira 2 car 3-1=2
l'élève 3 dira 3 car -(3/2)+9/2=3
l'élève 4 dira 4 etc.
l'élève 5 dira 5 etc.
l'élève 6 dira 6 etc.
l'élève 7 dira 7 etc.
l'élève 8 dira 8 etc.
l'élève 9 dira 9 etc.
l'élève 10 dira 10 etc.

FRiZMOUT · #9

Si j'ai bien compris l'énigme (désolé il est un peu tard ), on a la table suivante :

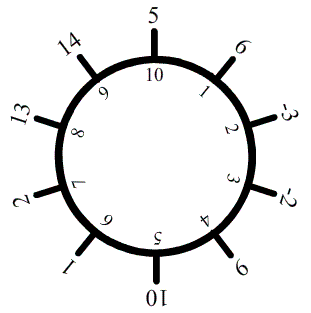
Pour les explications, euh, peut-être demain si j'ai le courage de sortir toutes mes combinaisons en LaTeX ^^

phil0156 · #10

Bonjour,

je propose en partant du premier collégien:
6, -3,-2,9,10,1,2,13,14,5
J'ai procédé par tâtonnement en utilisant excel pour faire varier les valeurs. ça a marché, peut-être y a-t-il un procédé plus logique? J'attends les réponses des cracks avec impatience!!
Bonne journée

letet · #11

non on peux pas car 1 n est pas une moyenne

emaths · #12

Oui on peut

Soient [latex]n_1,n2,\dots,n_{10}[/latex] les dix nombres choisis par ces collégiens. Les moyennes nous donnent les dix équations suivantes :
[TeX]\left\{\begin{eqnarray}
\dfrac{n_{10}+n_2}{2} & = & 1\\
\dfrac{n_{1}+n_3}{2} & = & 2\\
&\vdots&\\
\dfrac{n_{9}+n_1}{2} & = & 10\\
\end{eqnarray}\right.[/TeX]
Ensuite il suffit de former des combinaisons linéaires adéquates. Par exemple :
[latex]L_2-L_4+L_6-L_8+L_{10}[/latex] donne [latex]n_1=2-4+6-8+10=6[/latex].

On obtient ainsi les 10 nombres : 6, -3, -2, 9, 10, 1, 2, 13, 14, 5.

Golfc · #13

Si x est la moyenne de y et z, alors 2x=y+z. Voilà qui va simplifier nos deux systèmes à 5 inconnues.
Si A répond 1, la somme de J+B est égale à 2. etc...
J+B=2 A+C=4
B+D=6 C+E=8
D+F=10 E+G=12
F+H=14 G+I=16
H+J=18 I+A=20

Plus qu'à résoudre :
J-D=-4
J+D=14 -> 2J=10 J=5
A-E=-4
A+E=16 -> 2A=12 A=6

La suite est facile à déterminer :
A=6
B=-3
C=-2
D=9
E=10
F=1
G=2
H=13
I=14
J=5

Elle m'a plu !

naturel · #14

Les nombres choisis : 6, -3, -2, 9, 10, 1, 2, 13, 14 et 5

Vasimolo · #15

Bonnes réponses de: Bamby2 , dhrm77 , gabrielduflot , Palin01 , scrablor , FRiZMOUT , phil0156 , emaths , Golfc et naturel .

Toutes les méthodes proposées sont bonnes en voilà une avec deux équations à une seule inconnue :

On a [latex]2x+8=20[/latex] et [latex]2y+8=2 [/latex]donc [latex]x=6[/latex] et [latex]y=-3[/latex] , le reste suit .

Vasimolo

emmaenne · #16

naturel a écrit:
Les nombres choisis : 5, 6, -3, -2, 9, 10, 1, 2, 13 et 14

pour moi ce serait plutôt relatif

MthS-MlndN · #17

Autleaf a écrit quelque chose de joli, dommage qu'il se soit trompé dans la création de son système (erreur de second membre ET erreur dans la matrice du système).

scrablor · #18

Quitte à prendre des matrices, j'aurais choisi :
[TeX]\begin{pmatrix}
1 & 1 & 0 & 0 & 0\\
0 & 1 & 1 & 0 & 0\\
0 & 0 & 1 & 1 & 0\\
0 & 0 & 0 & 1 & 1\\
1 & 0 & 0 & 0 & 1\\
\end{pmatrix}*\begin{pmatrix}
a\\
c\\
e\\
g\\
i\\
\end{pmatrix}=\begin{pmatrix}
4\\
8\\
12\\
16\\
20\\
\end{pmatrix}[/TeX]
et
[TeX]\begin{pmatrix}
1 & 1 & 0 & 0 & 0\\
0 & 1 & 1 & 0 & 0\\
0 & 0 & 1 & 1 & 0\\
0 & 0 & 0 & 1 & 1\\
1 & 0 & 0 & 0 & 1\\
\end{pmatrix}*\begin{pmatrix}
b\\
d\\
f\\
h\\
j\\
\end{pmatrix}=\begin{pmatrix}
6\\
10\\
14\\
18\\
2\\
\end{pmatrix}[/TeX]

kosmogol · #19

Vasimolo a écrit:
Bonnes réponses de: Bamby2 , dhrm77 , gabrielduflot , Palin01 , scrablor , FRiZMOUT , phil0156 , emaths , Golfc et naturel .

Toutes les méthodes proposées sont bonnes en voilà une avec deux équations à une seule inconnue :
http://img518.imageshack.us/img518/9928/moyennes.jpg
On a [latex]2x+8=20[/latex] et [latex]2y+8=2 [/latex]donc [latex]x=6[/latex] et [latex]y=-3[/latex] , le reste suit .

Vasimolo

joli

MthS-MlndN · #20

Très très joli, même.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 21-08-2009 02:09:53

Dix moyennes consécuitves

#0 Pub

#2 - 21-08-2009 03:41:26

Dix moyenness consécutives

#3 - 21-08-2009 03:58:52

dix moyennzs consécutives

#4 - 21-08-2009 13:06:38

Dix moyennes consécuitves

#5 - 21-08-2009 15:35:18

Di moyennes consécutives

#6 - 21-08-2009 16:20:34

Dix moyennes consécutivs

#7 - 21-08-2009 18:01:51

dix moyennes consécutivrs

#8 - 21-08-2009 20:22:08

Dix moennes consécutives

#9 - 22-08-2009 00:17:12

diw moyennes consécutives

#10 - 22-08-2009 08:49:46

Dix mooyennes consécutives

#11 - 22-08-2009 20:31:34

Dix moennes consécutives

#12 - 23-08-2009 11:49:29

Dix myennes consécutives

#13 - 23-08-2009 16:19:08

DDix moyennes consécutives

#14 - 23-08-2009 16:34:10

Dix moynenes consécutives

#15 - 24-08-2009 09:01:40

Dix moyennees consécutives

#16 - 24-08-2009 09:18:07

Dxi moyennes consécutives

naturel a écrit:

#17 - 24-08-2009 12:05:29

Dix mooyennes consécutives

#18 - 24-08-2009 15:20:15

Dix moyennes consécuties

#19 - 31-08-2009 03:38:51

dix mouennes consécutives

Vasimolo a écrit:

#20 - 31-08-2009 11:56:19

Di xmoyennes consécutives

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums